In Tank Battle Field game, collision detection mostly applies in two cases:
- The primary tank (player tank) runs into a building, enemy or any other object on the ground
- Shells hitting the primary tank, the enemy units, building or other objects.
Main tank collision detection
As of this version of the game, the only moving vehicle on the field is the primary tank. Since it can move forward and backward, turns left and right, it is essential to be sure that any of these movements do not hit a solid object that denies the tank from changing position.
(it won't be realistic enough, nor interesting, to see the tank driving through buildings for instance).
So to be able to verify whether the tank hit something or not, we keep an eye on eight predefined points of the tank, and we check whether in the new position of the tank any of these points hit a solid object.
These points (called border points) are defined relatively to the center of the tank. For example the upper left corner has the coordinates x = - TankWidth/2 and y = TankLength/2 and so on for the other points.
Each time the tank moves or turns (rotates) the border points are computed in absolute coordinates taking into consideration the new position (including the rotation angle) that the tank it trying to move to.
Lets take an example. Consider that Xc, Yc are the coordinates of the center of the tank and Xul, Yul those of the upper left corner relatively to the tank center. When the tank moves the coordinates of the upper left corner in the absolute system will be:
AbsXul = Xc + (Xul * cosθ - Yul * sinθ)
AbsYul = Yc - (Xul * sinθ + Yul * cosθ)
where θ is the rotation angle of the tank
The above formula is a combination of a translation and a rotation transformations. (You can read more about transformations in the following wikipedia article "transformation matrix" )
The above has determined the border points of the tank. What remains is to check whether any of these points collided into a building. In other words, if any of these points came into intersection with building (or any other solid object) borders then we consider that a collision took place.
This suggests that we know the borders of these solid objects. In case of sprites, we know that they are always contained in a rectangle. However the rectangle might not accurately model the content of the sprite which might be of any shape. So the containing rectangle is not useful for a large number of cases which does not make it appealing. You can easily verify in the image below that the containing rectangle can quickly make the game unplayable.
In the image above, the tank can't move inside the containing rectangle which make the game unrealistic.
To solve this problem, we use polygons to model non-rectangular shapes such as this castle.
However this comes at a price of CPU power in order to try finding if any border point of the tank has crossed the polygon.
You may like to refer to this wikipedia article to know more about detection of a point inside a polygon.
The good news, is that not every thing requires a polygon, but there are cases where several rectangles might do the job. Telling that a point is inside a rectangle is by far faster than telling if it is inside a polygon. So, it is perfectly reasonable to model some objects using a series of rectangle as depicted in the image below.
In the above image, we modeled the house with two rectangles leaving the outdoors free for the tank to drive through.
Shells hit point
What makes tank games appealing is the ability to fire shells on targets. Determining how and where a shell hit a target is also a collision detection problem.
Mathematically this problem can be reduced to finding the intersection point between two lines.
The scenario where the tank fires on the castle,
can be reduced to the following intersection of two lines.
Here we consider that there are two lines defined as
Line A: y = a*x + b
Line B: y = c*x + d
Finding the hit point comes to find the intersection point of Line A with Line B. We define this intersection point by xi, yi. The solution becomes
xi = (b - d) / (c - a)
It follows that yi = a*xi + b
Certainly enough if the slopes represented by a and c are equal, this means the two lines are parallel and won't be intersecting thus the xi won't be determined since the denominator will be zero.
Mathematically this is valid solution. However this is not necessarily true in the game, because in maths the lines are infinite, so in case they are not parallel they will eventually intersect at some point. But in the game the shell has a limited range and the target's borders are also constrained in length. To be valid the intersection point must necessarily be with the valid range of each line.
Back to our previous example, if we say that the Line A stretches between point A1 and point A2 and Line B goes from point B1 to point B2. So in order for the intersection point given by (xi, yi) to be valid, the following relations should be true.
xi >= A1.x && xi <= A2.x assuming that A1.x <= A2.x
and
xi >= B1.x && xi <= B2.x assuming that B1.x <= B2.x
if the above relations are not true we might be in situation like in the image below, where the intersections happens outside the valid ranges.
Special case
We might think that we are done with the hit point. But still this not true yet!
Actually the equations handling the shell trajectory is based on time and velocity.
They have the following form:
x = Vx * t + x0
y = Vy * t + y0
where Vx and Vy are the components of the shell velocity along the x-axis and the y-axis while the x0, y0 is the point of origin (in other terms the tank).
The coordinates of the shell location are updated on each loop turn. This represents a problem since the update occurs every laps of time. So the graphical representation of the shell is discrete and not continuous.
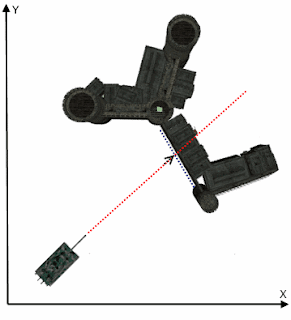
The image below shows in grey the theoretical (continuous) trajectory of the shell, and in red dots the reel location of the shell over the time.
As you can see there is no way to verify that the shell hit the house by following the red dots alone. Actually the red dot never happen to appear inside the house borders.
To solve this issue, after each update of the shell position we check for intersection between the line formed by the starting point of the shell (position of the tank when it fired) and the latest shell position and the borders of the house.
It appears that for the first two shell positions there is no intersection. But on the third time we notice two intersections represented by the red crosses (X).
Naturally we chose the intersection that is closer to the tank as the hit point or the point of impact then we trigger the explosion sequence. Eventually we ignore the second intersection point and we don't show the third shell position on the screen.
Performance issue
So far the game does not contain too many objects nor requires too many computations that might affect performance. However, to do the things "right", we do take performance topic into consideration.
When detecting collision, we have to check the tank or shell position against every other solid object on the map. So in order to avoid using costly line intersections or polygons checks we first start by simply finding out what containing rectangles (surrounding objects) intersect with the rectangle formed by the tank position as first corner and the shell position as diagonally opposed corner (see image below). This way using cheap technique we can gather all solid objects that potentially lie in the way of the shell. Then we start testing using the more costly line intersection method on this reduced set of objects.
On the other hand, when seeking to find if the tank is about to collide with other solid objects, we start by checking for candidate objects by verifying if the tank crossed their containing rectangle, then we run a more accurate test using the point-in-polygon technique to find out if the tank really collided with one of them.
The demo
That's it for today, as always you can check the latest demo by going to http://tankbattlefield.eu.pn
D3GGQP7C7BF3









No comments:
Post a Comment